MidPoint development of is full of interesting software problems – be it management of long-running tasks, integration of third-party workflow engine, devising a flexible authorization mechanism, creating a GUI that adapts to the customizable data model, or many others. However, the following one in particular reminded me of my happy student years at the faculty of mathematics and physics: computing the transitive closure of the organizational structure graph.
What’s it about?
MidPoint cares about the organizational structure, or, better said – structures. A company can have a number of divisions, each of which could be split into departments. In public governance scenario, a country can be divided into regions, regions into counties, and in each county there can be cities and villages. Or, a university can have faculties; faculties can have departments, and within departments there can be any smaller organizational units, as dictated by local habits. Any person can then belong to one or more such units. Moreover, there can be structures laying over the above-mentioned ones. For example, there can be a set of projects, forming again a tree (or more trees). The structure of study programs at the university can also form such an overlaying structure.
We want to be able to point at any organization (it’s a midPoint term for anything that is part of the organizational structure) O in such a set of hierarchies and ask questions like “does user X belong to O or any of its suborganizations?” or “give me a list of users of age under 35, belonging to O or any of its suborganizations.”
It is easy to see that what we have here is a directed acyclic graph, also known as DAG. Let’s call it G. G consists of two sets: V and E. V is the set of vertices of this graph; these are organizations and persons. E is the set of edges. An edge e from vertex v1 to vertex v2 is in E if organization or user v1 “belongs to” organization v2 (we would say that v2 is a parent of v1). What we need is the transitive closure of this graph, i.e. a graph G* = (V, E*), which has the same set of vertices as V and contains an edge e from vertex v1 to vertex v2 if and only if v2 is an ancestor (i.e. parent or grand-parent or grand-grand-…-parent) of v1.
If we would have G* available, then it would be very easy to answer questions posed above:
- Answering the question “does user X belong to O or any of its suborganizations?” would become a simple query to see if there is an edge from X to O in G*.
- Answering the question “give me a list of users of age under 35, belonging to O or any of its suborganizations” would consist of getting all elements U such that there is an edge from U to O in G*, U is a user, and U is of age under 35.
But… how to compute the closure?
There are many nice algorithms for computing the transitive closure of a graph, for example the Floyd-Warshall algorithm. However, this algorithm (and many other ones) expects that the graph is fully stored in main memory. And, what is worse, the time needed for the computation is just too large for large graphs.
The more practical approach is to store a transitive closure alongside the original graph. When changing the graph, we would make a corresponding change in the closure. Our repository is implemented as a SQL database, so both original graph and its closure would be represented as database tables.
At first, we implemented an algorithm proposed by Dong et al [1]. Its main idea can be explained like this: when adding an edge v1 → v2 into G, add to G* all edges x → y such that x → v1 and v2 → y are already in G*. It’s obvious: if there is a path from x to v1 and a path from v2 to y, certainly there will exist a path from x to y, because v1 is now connected to v2. And the other way around: any “new” path from x to y would comprise one “old” path from x to v1, then “new” edge v1 → v2 and then some “old” path from v2 to y. This can be implemented as an SQL join, followed by some commands aimed to insert those rows to G* that aren’t already there.
The removal of edge from G is a bit more complex: the algorithm computes a table SUSPECTS that contains all edges x → y such that there was a path from x to y going through edge being deleted (v1 → v2). Then it computes a TRUSTY table containing all edges that are for certain untouched by the removal of the edge v1 → v2. And finally, as authors have proven, new transitive closure contains all paths that are created by concatenation of up to three subpaths from the TRUSTY table.
Unfortunately, this “removal” side of the algorithm takes just too long time to execute. Much longer than is acceptable in midPoint.
Is that the best we can do?
Certainly not. After slight googling I’ve found a very interesting article, referring to a chapter in the SQL patterns book by Vadim Tropashko [2]. Here comes the idea:
Each graph can be represented by an adjacency matrix A = (aij) where aij = 1 or 0, depending on whether there is an edge vi → vj or not (i, j range from 1 to N, where N is the number of vertices). If we compute the following:
T = A + A2 + A3 + A4 + …
we will get a matrix T = (tij) containing information about the number of paths from any vertex vi to any other vertex vj in G! It is not so hard to see that:
- A = (aij) contains the number of paths of length 1 (i.e. edges) from vi to vj.
- A2 = A*A = (a(2)ij) contains the number of paths of length 2 from vi to vj. It is so because a’ij = ai1*a1j + ai2*a2j + ai3*a3j + … + aiN*aNj. So we take the number of paths of length 1 from vi to v1 (it is 0 or 1 in this case, but that’s not important), multiply it by the number of paths of length 1 from v1 to vj (again 0 or 1) and this is the number of paths of length 2 from vi to vj going through v1. We do the same for v2, …, vN and then by adding these numbers together we get the number of all paths of length 2 from vi to vj i.e. a(2)ij.
- In a similar way, Ak = (a(k)ij) contains the number of paths of length k from vi to vj for any k.
It is clear that T is very close to the transitive closure, isn’t it? If we replace all non-zero numbers in it by 1, we will get the adjacency matrix of the transitive closure graph.
This is interesting, but not directly helpful.
As Tropashko shows using simple algebraic operations, changing adjacency matrix A of graph G by adding an edge e, represented by matrix S, i. e.
A → A + S
changes the transitive closure matrix T to a new value of T + T*S*T, i. e.
T → T + T*S*T
and this is something that can be computed using SQL without much problems!
What is even more delighting is that the reverse operation, i.e. edge removal, is of about the same complexity:
A → A – S;
T → T – T*S*T.
SQL implementation of this computation is really simple. T*S*T can be computed using one join. T + T*S*T is then one upsert (update+insert), and T – T*S*T is done as update+delete. Details are more than understandably described in Tropashko’s book.
We improved the Tropashko’s algorithm a little bit by allowing adding/removal of more edges at once. The only condition is that they are “independent” in such a way that no path would go through two or more edges added/removed in one step. Also, we added special treatment for some situations, namely adding a node with one parent and no children and removing a node without children.
The implementation
The implementation was quite straightforward. Each of 5 supported databases (H2, MySQL, PostgreSQL, Oracle, Microsoft SQL Server) has its own specifics concerning how to deal with temporary tables, how to write upsert/merge command, how exactly to write update and delete commands to achieve the best performance, and how to deal with concurrent access to the closure table.
The final step was realization that by moving users out of the organizational graph we could make closure table updates much more efficient (by reducing its size substantially), while making queries slightly slower (by introducing a join between the closure and user-org relation table).
Production-ready code can be seen in OrgClosureManager class.
Preliminary performance evaluation
We have done a preliminary performance evaluation of our implementation on MySQL and PostgreSQL databases. It was done by creating a sequence of graphs of the following sizes:
| Level 1 | Level 2 | Level 3 | Level 4 | Level 5 | Orgs | Closure size |
| 1 | 2 | 3 | 4 | 5 | 153 | 1K |
| 2 | 2 | 3 | 4 | 5 | 306 | 3K |
| 4 | 2 | 3 | 4 | 5 | 612 | 9K |
| 4 | 4 | 3 | 4 | 5 | 1220 | 21K |
| 4 | 8 | 3 | 4 | 5 | 2436 | 49K |
| 8 | 8 | 3 | 4 | 5 | 4872 | 116K |
| 8 | 16 | 3 | 4 | 5 | 9736 | 252K |
| 4 | 8 | 6 | 8 | 10 | 17124 | 379K |
“Level 1″ column indicates how many root nodes are there. “Level 2..5″ colums say how many children at a particular level (2..5) were created for each parent node residing at the upper level. “Orgs” is the total number of vertices in the graph, and “Closure size” gives an approximate number of records in the closure table. It is approximate, because the graph was generated by a randomized algorithm, and while the number of parents for each org was given (for levels 1 to 5 these are 0, 1, 2, 3, and 3, respectively), by creating the graph in a depth-first way, some of the child-parents links were not created, as there were not enough parents existing yet.
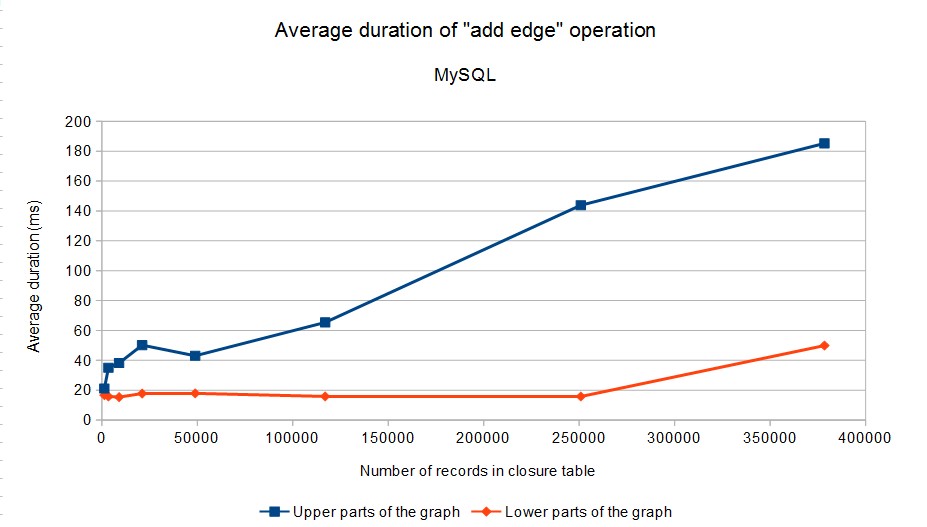
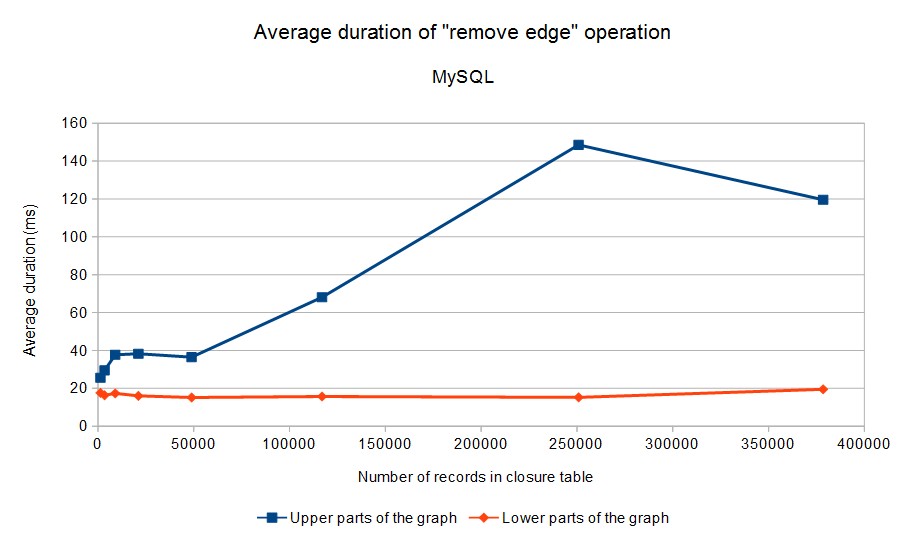
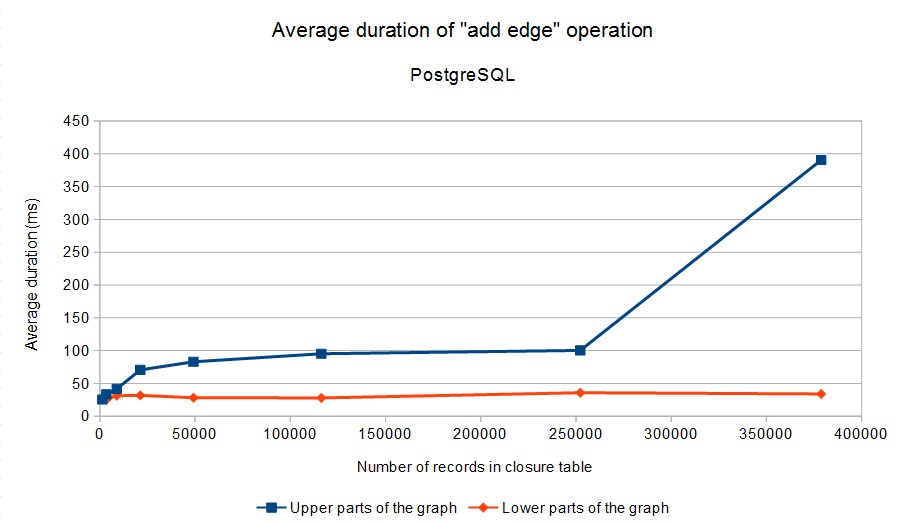
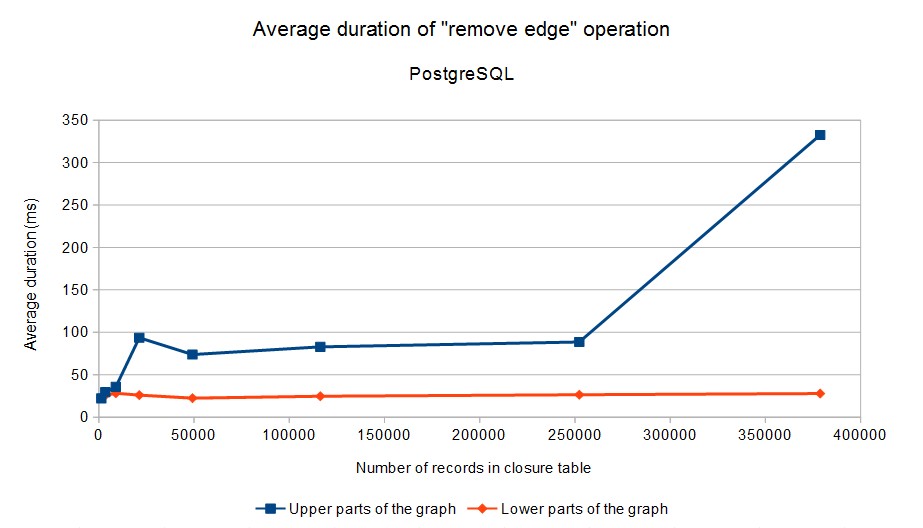
Here are the results. Because operation duration strongly depends on the number of affected rows in the closure table, we have divided operations into two categories: (1) operations in the “upper part” of the graph (levels 1, 2, 3 in our case), (2) operations in the “lower part” of the graph (levels 4 and 5). These two categories are distinguished in the graphs below (click to enlarge):
Note that the average time required to add/delete an edge in the lower parts of the graph (where majority of operations can be expected to occur) does not exceed 50 milliseconds in all cases.
Calc sheet with the results is here.
Tests were executed by running (appropriately configured) OrgClosurePerformanceTest2 class. The configuration of database servers had to be tuned a bit. Basically, the memory available to the servers had to be increased. The numbers related to MySQL and PostgreSQL are absolutely not meant as a comparison of these databases – for example, the engines are not tuned in the same way. They are only shown here as an indication that the algorithm works on more than one specific database engine. By tuning the engines appropriately (e.g. by allowing them to use more memory or tweaking other parameters) we could perhaps get to even better results. However, we consider the results presented here to be are good enough for our purposes.
Conclusion
We have shown here a basic idea of two existing transitive closure maintenance algorithms and some notes on our implementation of one of them, along with a preliminary performance evaluation. You can freely inspire yourself by looking at the source code (albeit some of the code is really midPoint-specific). Any suggestions or improvements are more than welcome!
Life of a software developer often brings surprising and much pleasuring moments. Meeting years-forgotten pieces of graph theory and even linear algebra during development of an identity management tool is definitely one of them. ![]()
References
[1] Guozhu Dong, Leonid Libkin, Jianwen Su and Limsoon Wong: Maintaining the transitive closure of graphs in SQL. In Int. J. Information Technology, vol. 5, 1999.
[2] Vadim Tropashko: SQL Design Patterns: Expert Guide to SQL Programming. Rampant Techpress, 2007. ISBN 978-0977671540.
Volunteers, students interested in academic research in identity management could find more information at:
https://wiki.evolveum.com/display/midPoint/Academia